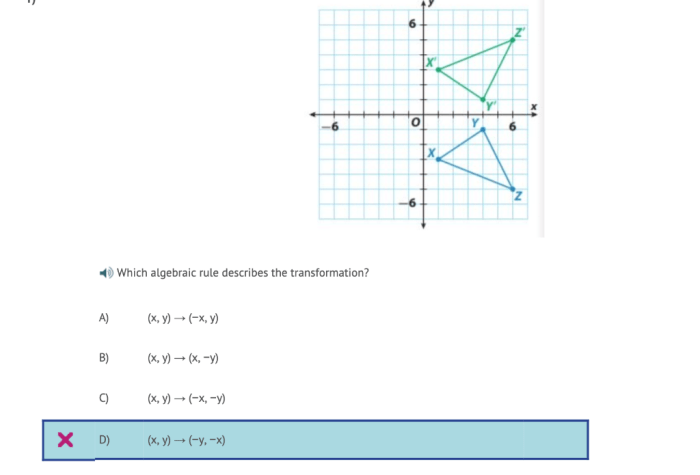
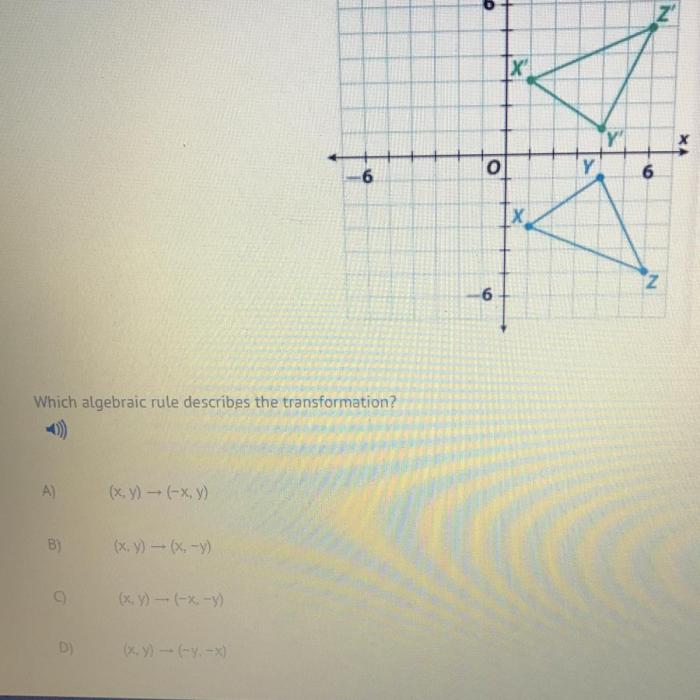
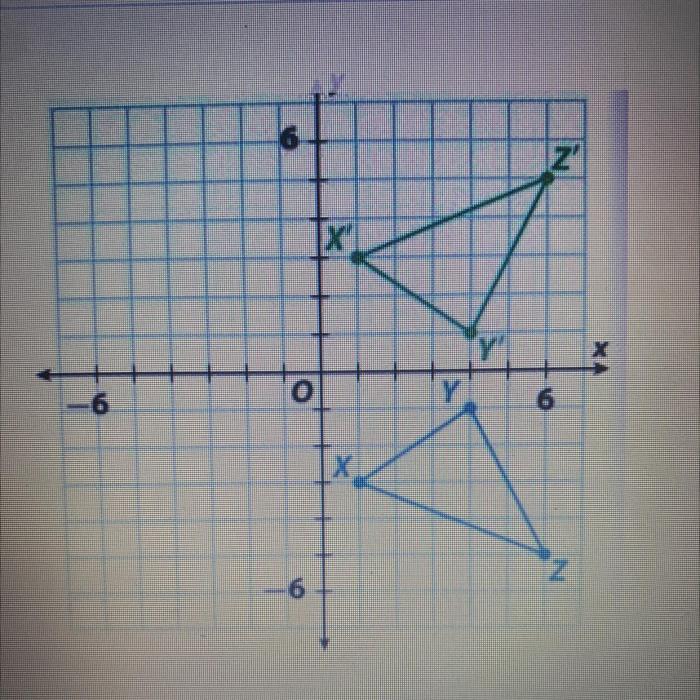
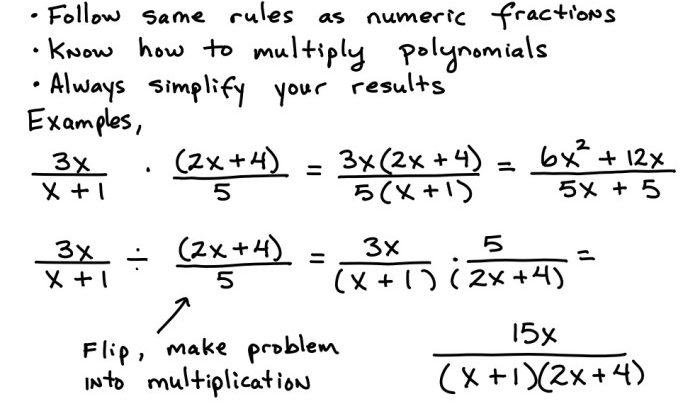Embarking on an exploration of which algebraic rule describes the transformation, we uncover a fascinating and intricate realm where mathematical expressions undergo remarkable changes. From the outset, we delve into the diverse algebraic rules that govern these transformations, setting the stage for a comprehensive understanding of their properties and applications.
As we navigate the intricacies of algebraic transformations, we will encounter a spectrum of rules, each possessing unique characteristics and serving distinct purposes. Through a comparative analysis, we will unravel the nuances of these rules, empowering us to make informed choices when seeking to transform expressions effectively.
Algebraic Transformations: Which Algebraic Rule Describes The Transformation
Algebraic transformations are mathematical operations that alter the form or structure of an algebraic expression while preserving its value. They are used to simplify expressions, solve equations, and perform various mathematical manipulations.
Types of Algebraic Transformations, Which algebraic rule describes the transformation
- Addition and Subtraction
- Multiplication and Division
- Exponents and Radicals
- Logarithms
- Factoring
- Completing the Square
- Quadratic Formula
Identifying Algebraic Rules
Algebraic transformations are governed by specific rules that describe how operations can be performed. These rules include:
| Rule | Description | Application |
|---|---|---|
| Commutative Property | Changing the order of terms does not affect the value. |
Addition and Multiplication |
| Associative Property | Grouping terms in different ways does not affect the value. |
Addition and Multiplication |
| Distributive Property | Multiplying a term by the sum of two terms is equivalent to multiplying it by each term individually. |
Multiplication over Addition |
| Identity Property | Adding or multiplying by 0 or 1 does not change the value. |
Addition and Multiplication |
| Inverse Property | Adding or multiplying by the inverse of a number results in 0 or 1. |
Addition and Multiplication |
| Exponent Laws | Rules for manipulating exponents, such as product rule and power rule. |
Exponents |
Rule Application in Transformation
- Addition and Subtraction:Combine like terms, eliminate zero terms, and simplify expressions.
- Multiplication and Division:Apply distributive property, simplify fractions, and perform cross-multiplication.
- Exponents and Radicals:Use exponent laws, simplify radicals, and rationalize denominators.
- Logarithms:Apply logarithmic properties, convert between exponential and logarithmic forms, and solve logarithmic equations.
- Factoring:Decompose expressions into factors, simplify radicals, and solve quadratic equations.
- Completing the Square:Convert quadratic expressions into perfect squares, solve quadratic equations, and find the vertex of a parabola.
- Quadratic Formula:Solve quadratic equations in the form ax 2+ bx + c = 0.
Rule Selection for Transformation
Selecting the appropriate algebraic rule for a transformation depends on the desired outcome and the structure of the expression. Consider the following factors:
- Operation to be performed:Identify the mathematical operation involved, such as addition, multiplication, or exponentiation.
- Form of the expression:Examine the structure of the expression to determine if it can be simplified using specific rules, such as factoring or completing the square.
- Goal of the transformation:Determine the desired outcome of the transformation, such as simplifying the expression, solving an equation, or finding a specific value.
Query Resolution
What is the significance of algebraic rules in transformations?
Algebraic rules provide a systematic framework for describing and performing transformations, ensuring consistency and accuracy in mathematical operations.
How do I determine the most suitable algebraic rule for a given transformation?
The selection of an appropriate algebraic rule hinges on the specific transformation being performed and the desired outcome. Decision trees or flowcharts can guide this selection process effectively.
Can algebraic rules be applied to complex mathematical expressions?
Yes, algebraic rules can be applied to expressions of varying complexity. By breaking down complex expressions into simpler components, we can systematically apply the appropriate rules to achieve the desired transformation.